728x90
❤️ 배운 것
KNN Classification
Feature Space: x 값(col)이 표시된 공간, feature space는 n차원으로 확장 가능
feature = x, target class = y
k-nearest : 타겟 클래스를 모르는 새로운 데이터가 들어올 때 기존의 샘플을 보고 그에 따라 새로운 값의 target(y) 값을 예측하는 방법
가장 가까운 k개의 데이터를 기준으로 값을 분류함
k는 = 1, 3, 5 .. 홀수로 지정
ex) k가 3일 때,
제일 가까운 3개의 데이터중 2개가 no이고, 1개가 yes 라면
target(y)는 다수결의 원칙에 따라 no로 분류
Euclidean distance
Euclidean(a,b)=√m∑i=1(a[i]−b[i])2
Manhattan distance
Manhattan(a,b)=m∑i=1abs(a[i]−b[i])
- Euclidean distance가 길이 차이를 더 잘 반영함

KNN에서 가장 가까운 k개 데이터를 구하는 방법은 새로운 데이터의 좌표와 기존 좌표간의 euclidean distance를 계산
그 후 오름차순으로 정렬하여 가장 작은 d 값부터 k개만큼 추출
K 값은 하이퍼 파라미터
decision boundary: 결정경계
KNN 코드 실습
- 정규분포로부터 100개의 랜덤 값 추출하여 도수분포표 그리기
import numpy as np
import matplotlib.pyplot as plt
def code1_normal_histogram():
n_data = 100
x_data = np.random.normal(loc=5, scale=5, size=(n_data,))
fig, ax = plt.subplots(figsize=(5, 5))
ax.hist(x_data, rwidth=0.9)
fig.tight_layout()
- (100,2) 크기의 랜덤 데이터셋 만들기 (stack, hstack, concatenate 등)
def code2_dataset_1cluster():
# 평균이 (5, 3)이고, 표준편차가 x, y 방향으로 모두 1인 (100, 2) dataset 만들기
n_data = 100
x_data = np.random.normal(5, 1, size=(n_data,))
y_data = np.random.normal(3, 1, size=(n_data,))
data_ = np.stack([x_data, y_data], axis=1)
print(x_data.shape, y_data.shape)
print(data_.shape)
# 다른 방법
# data_ = np.concatenate((x_data, y_data), axis=1)
data = np.random.normal(loc=[5, 3], scale=[1, 1], size=(n_data, 2))
print("mean: ", np.mean(data, axis=0))
print("std: ", np.std(data, axis=0))
'''
(100,) (100,)
(100, 2)
mean: [5.01125342 3.15212465]
std: [1.094432 1.0596849]
'''- centroid 중심점으로부터 무작위 산점도 그리기
def code3_random_centroid():
# 무게중심을 random하게 만들고, dataset의 모양이 (100, 2)가 되도록 만들어 scatter plot 시각화
n_data = 100
centroid = np.random.randint(-5, 5, size=(2,))
# data = np.random.normal(loc=[centroid[0], centroid[1]], scale=[5, 5], size=(n_data, 2))
# data의 col과 size의 col만 맞추면 dataset 그대로 loc에 설정하면 됨
# scale도 숫자로 작성하면 모든 값에 동일한 표준편차가 적용됨
data = np.random.normal(loc=centroid, scale=1, size=(n_data, 2))
print(data.shape) # (100, 2)
fig, ax = plt.subplots(figsize=(5, 5))
ax.scatter(x=centroid[0], y=centroid[1], color="red")
ax.scatter(x=data[:, 0], y=data[:, 1])- loc의 col과 size의 col만 맞추면 dataset 그대로 loc에 설정하면 됨
- scale도 숫자로 작성하면 모든 값에 동일한 표준편차가 적용됨

- 4개의 서로다른 클래스로 구성된 랜덤데이터셋 시각화
def get_data_from_centroid(centroid, n_data):
data = np.random.normal(loc=centroid, scale=1, size=(n_data, 2))
return data
def code4_knn_x_dataset():
# 4 class, class마다 100개의 점을 가지는 dataset 만들기 (400, 2) # class들의 centroid는 랜덤하게
np.random.seed(0)
n_classes = 4
n_data = 100
centroids = np.array([np.random.uniform(low=-20, high=20, size=(2,)) for x in range(n_classes)])
target_cls = np.array([i for i in range(n_classes) for _ in range(n_data)])
data = None
for i, centroid in enumerate(centroids):
if i == 0:
data = get_data_from_centroid(centroid, n_data)
continue
curr_dataset = get_data_from_centroid(centroid, n_data)
data = np.vstack([data, curr_dataset])
fig, ax = plt.subplots(figsize=(5, 5))
ax.scatter(x=data[:, 0], y=data[:, 1], c=target_cls, alpha=0.5)
cent_arr = centroids.reshape(-1, 2)
ax.scatter(x=cent_arr[:, 0], y=cent_arr[:, 1],
marker='x', color='purple', s=100)
def code4_knn_x_dataset2():
# 예제 코드
n_classes = 4
n_data = 100
data = []
centroids = []
for _ in range(n_classes):
centroid = np.random.uniform(low=-10, high=10, size=(2,))
data_ = np.random.normal(loc=centroid, scale=1, size=(n_data, 2))
centroids.append(centroid)
data.append(data_)
centroids = np.vstack(centroids)
data = np.vstack(data)
fig, ax = plt.subplots(figsize=(5, 5))
for class_idx in range(n_classes):
data_ = data[class_idx * n_data: (class_idx + 1) * n_data]
ax.scatter(data_[:, 0], data_[:, 1], alpha=0.5)
for centroid in centroids:
ax.scatter(centroid[0], centroid[1], c='purple', marker='x', s=100)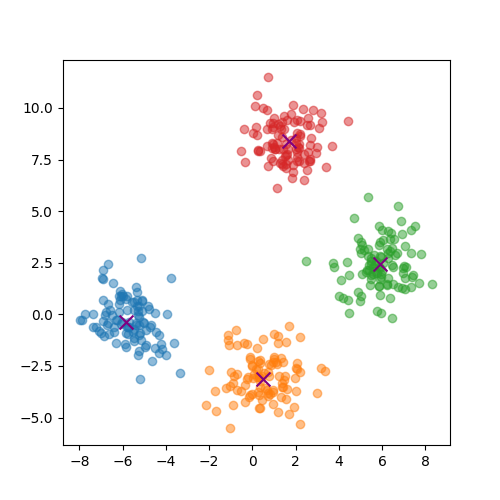
- 모든 값이 0~4, 모양이 (100,)인 ndarray n_classes = 4
def code5_targets():
# 모든 값이 0~4, 모양이 (100,)인 ndarray n_classes = 4
n_data = 100
data = []
for i in range(n_classes):
# data_ = i * np.ones(n_data,)
data_ = np.full(n_data, i)
data.append(data_)
data = np.hstack(data)
# data = np.concatenate(data)
print(data.shape)- knn random dataset 만들기
def get_data_from_centroid(centroid, n_data):
data = np.random.normal(loc=centroid, scale=3, size=(n_data, 2))
return data
def code6_knn_dataset(n_classes, n_data):
np.random.seed(8)
centroids = np.array([np.random.uniform(low=-10, high=10, size=(2,)) for x in range(n_classes)])
target_cls = np.array([i for i in range(n_classes) for _ in range(n_data)])
data = None
for i, centroid in enumerate(centroids):
if i == 0:
data = get_data_from_centroid(centroid, n_data)
continue
curr_dataset = get_data_from_centroid(centroid, n_data)
data = np.vstack([data, curr_dataset])
return data, target_cls, centroids- KNN: 테스트 데이터와 dataset에 들어있는 샘플들 사이의 거리 구하기
def code7_euclidean_distances():
# KNN: 테스트 데이터와 dataset에 들어있는 샘플들 사이의 거리 구하기
X, y, centroids = code6_knn_dataset(n_classes=4, n_data=100)
X_te = X[0]
euclidean_d = np.sqrt(np.sum((X - X_te)**2, axis=1))
return X, y, centroids, X_te, euclidean_d- numpy의 broadcasting 기능을 활용하면 for문을 생략하고 작성 할 수 있음
- test data 분류
def code8_classify(K=None):
# test data가 어떤 클래스에 속하는지 구하기
if K is None:
K = 6
else:
K += 1
X, y, centroids, X_te, e_dists = code7_euclidean_distances()
ascending_idx = np.argsort(e_dists)
# make full data
e = e_dists.reshape(-1, 1)
y = y.reshape(-1, 1)
full_data = np.hstack((X, e, y))
full_data_ascd = full_data[ascending_idx]
# get k values and predict
uniques, cnts = np.unique(full_data_ascd[:K, -1], return_counts=True)
uniques = uniques.astype(dtype=np.int64)
most_frequent = np.argmax(cnts)
y_hat = uniques[most_frequent]
# print(y_hat) # 0
results = dict()
results["K"] = K
results["X"] = X
results["y"] = y
results["X_te"] = X_te
results["e_dists"] = e_dists
results["full_data"] = full_data
results["K_data"] = full_data_ascd[:K, :]
results["unique_cnts"] = (uniques, cnts)
results["centroids"] = centroids
results["y_hat"] = y_hat
return results- main 루틴에 변수 처리를 안해서 임시로 result dict를 return 시켰음
- 추후에 리팩토링 요망
- KNN visualization (in progress)
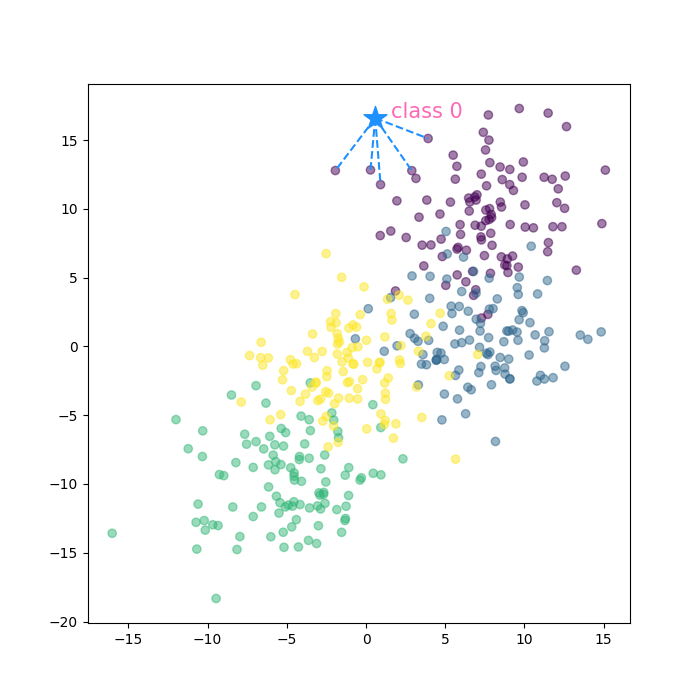
def code9_knn_visualization_tmp():
prediction = code8_classify(5)
K = prediction["K"]
X = prediction["X"]
y_hat = prediction["y_hat"]
k_data = prediction["K_data"]
X_te = prediction["X_te"]
fig, ax = plt.subplots(figsize=(7, 7))
# all data
ax.scatter(x=prediction["X"][:, 0], y=prediction["X"][:, 1], c=prediction["y"], alpha=0.5)
# to predict
ax.scatter(x=X_te[0], y=X_te[1], marker="*", s=300, color="dodgerblue")
ax.text(x=X_te[0]+1, y=X_te[1], s=f"class {y_hat}", color="hotpink", size=15)
# k nearest data
for i in range(len(k_data)):
curr_x = k_data[i, 0]
curr_y = k_data[i, 1]
ax.plot([X_te[0], curr_x], [X_te[1], curr_y], 'k--', color="dodgerblue")- decision boundary를 제외하고, 전체 산점도 및 test 데이터의 K-nearest 인 datapoint와의 라인플롯까지 작성함
💛 배운점/느낀점
- KNN의 개념 및 원리를 학습함
- numpy broadcasting을 실제 ndarray 연산하는 코드에 활용
- 내일은 decision boundary 코드 작성 예정
반응형
'Education > 새싹 TIL' 카테고리의 다른 글
| 새싹 AI데이터엔지니어 핀테커스 6주차 (목) - Kmeans, Decision Tree 해부 (진짜열심히했음) (0) | 2023.10.12 |
|---|---|
| 새싹 AI데이터엔지니어 핀테커스 6주차 (수) - KNN(full code) (1) | 2023.10.11 |
| 새싹 AI데이터엔지니어 핀테커스 5주차 (금) - Boxplot, Numpy (1) | 2023.10.06 |
| 새싹 AI데이터엔지니어 핀테커스 5주차 (목) - matplotlib (3) (1) | 2023.10.05 |
| 새싹 AI데이터엔지니어 핀테커스 5주차 (수) - matplotlib (2) (1) | 2023.10.04 |