행렬
스칼라 < 벡터 < 행렬 < 텐서
대각 행렬 (diagonal matrix)
단위 행렬 (identity matrix)
전치 행렬 (transposed matrix)
행렬의 스칼라곱: 행렬에 스칼라 2를 곱한다는 것은 행렬을 구성하는 벡터 길이가 두배로 길어진다는 뜻
행렬곱: (m x k) x (k x n) = (m x n)
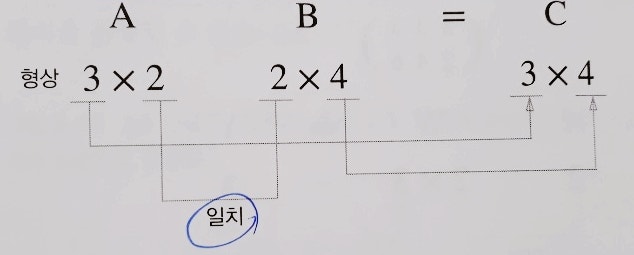
원소곱: 동일 위치 원소를 서로 곱하는 방법 -> 딥러닝 최적화 알고리즘에 자주 사용
matrix element multiplication

행렬식: 행렬을 구성하고있는 벡터로 만들 수 있는 도형의 부피를 계산한다는 의미
역행렬
내적
벡터+백터 = 스칼라
<> 혹은 · 도트곱으로 표현
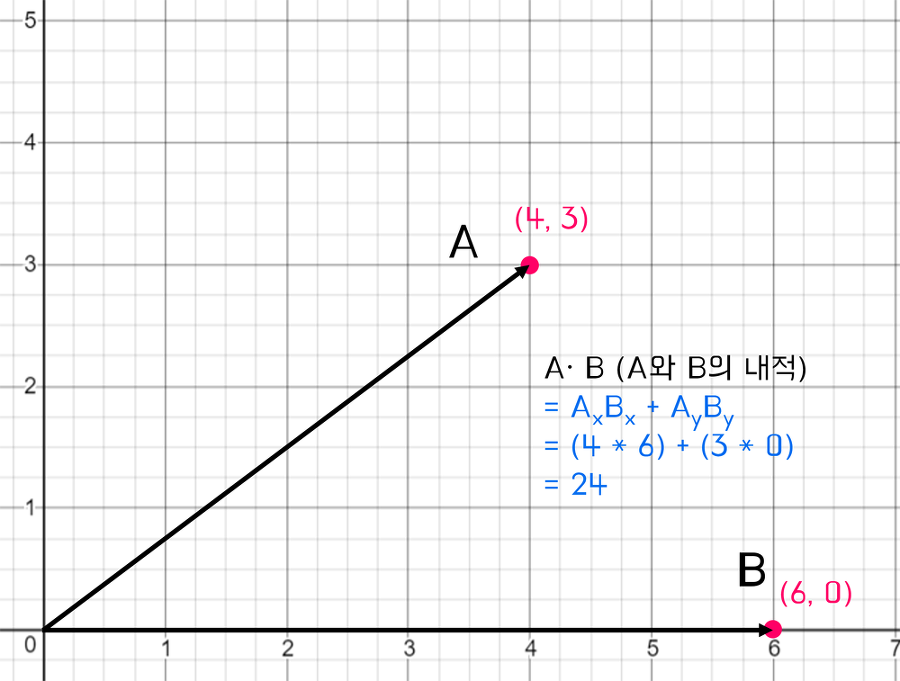
내적은 벡터의 길이(norm)을 구하거나 벡터 사이의 관계 파악 가능
- 내적>0이면 두 벡터 사이의 각도 < 90
- 내적<0이면 두 벡터 사이의 각도 > 90
- 내적=0이면 두 벡터 사이의 각도 = 0
벡터의 길이 : ||u|| 내적값의 제곱근

좌표 : (|v| cos 𝛉, |v| sin 𝛉)
참고) sin cos tan
정사영(projection): 한 벡터가 다른 벡터에 수직으로 투영하는 것 = ||u|| cos 𝛉
u, v 벡터가 있을 때 v를 x축이라고 생각하고 u 벡터에서 수직으로 선을 내리는 것임
내적은 서포트 벡터 머신과 관련 있음
선형 변환
선형변환(linear transformation): 좌표 평면에 벡터를 확대 ,축소 회전, 반사등 변환하는 것
랭크, 차원
벡터 공간
기저: 벡터 공간을 생성하는 선형 독립인 벡터들
부분공간
스팬(span)
차원(dimension): 기저 벡터의 개수
랭크(rank): 열벡터에 의해 span된 벡터 공간의 차원
직교 행렬
직교행렬(orthogonal matrix): 어떤 행렬의 행벡터와 열벡터가 유클리드 공간의 정규 직교 기저를 이류는 행렬
특이값 분해
닮음: P-1 A P = B
직교 대각화
고윳값 분해(eigenvalue decomposition) : 정사각 행렬 대상
특이값 분해(singular value decomposition) : 대상 행렬을 mxn 행렬로 일반화 시킨 것, PCA 같은 차원축소 분야에서 사용
'AI > Books' 카테고리의 다른 글
| 선형대수와 통계학으로 배우는 머신러닝 - Chap9 앙상블 학습 (0) | 2023.12.25 |
|---|---|
| 선형대수와 통계학으로 배우는 머신러닝 - Chap8 지도 학습 (1) | 2023.12.25 |
| 선형대수와 통계학으로 배우는 머신러닝 - Chap7 손실함수 (0) | 2023.12.25 |
| 선형대수와 통계학으로 배우는 머신러닝 - Chap6 머신러닝 데이터 라이브러리 (Scikit-Learn) (0) | 2023.12.25 |
| 선형대수와 통계학으로 배우는 머신러닝 - Chap4 머신러닝을 위한 통계학 및 파이토치 (1) | 2023.12.25 |

