새싹 AI데이터엔지니어 핀테커스 10주차 (금) - Loss Function & Differentiation

2023-11-10 47th Class

Loss Function

#️⃣ 손실함수

손실(Loss)란 모델의 예측값과 실제 정답의 차이를 의미

[1] Model’s Prediction

모델에 x가 입력되면, 여러 레이어를 거쳐 최종 출력 을 만듦
binary classification이라면 => 0 < y < 1 라는 의미

Binary Crossentropy 에서

1. Dataset의 label은 0과 1로 이루어져 있음
2. Model은 확률값을 출력

ex.1) Face ID Model
사람의 얼굴 이미지를 입력값으로 넣어서 모델의 예측값이 나옴
1에 가깝게 나오면 사용자로 예측하고
0에 가깝게 나오면 사용자가 아닌 것으로 예측함

[2] Loss Function

• Loss = 모델의 예측값 y hat과 실제 정답 y의 차이
• Loss Function = Loss를 계산하는 함수
• 이 loss 값은 parameter을 학습할 때 사용됨

Lloss Function에서

1. 정답 y와 모델의 출력 y hat이 비슷하면 j ≈ 0,
2. 차이가 크면 j → ∞

#️⃣ Binary Crossentropy

[1] 예측값과 loss의 관계

loss function이 binary cross entropy이고,
실제값(y), 예측값(yhat)으로 구한 loss가 J 라면

	y=0	y=1
yhat ≈ 0	J ~ 0	J → ∞
yhat ≈ 1	J → ∞	J ≈ 0

• 1. y=1,
  • a) y가 1일때, 이 0에 가까워지면 오차는 무한대로 발산
  • b) y가 1일때, 이 1에 가까워지면 오차는 0에 수렴
• 2. y=0,
  • a) y가 0일때, 이 0에 가까워지면 오차는 0에 수렴
  • b) y가 0일때, 이 1에 가까워지면 오차는 무한대로 발산

#️⃣ Binary Cross Entropy

• (1) 와 (2) 를 더한 식
• y=0이 입력되면 (1)은 0으로 바뀌며, (2)는 로 바뀜
• y=1이 입력되면 (1)은 로 바뀌며, (2)는 0으로 바뀜

BCE는 정답이 0, 1이고 출력이 확률일 때 두 값의 차이를 연산해주는 함수

Binary Crossentropy

class BCELoss:  
    def forward(self, y, pred):  
        J = -(y * np.log(pred) + (1 - y) * np.log(1 - pred))  
        return J  
  
  
loss_function = BCELoss()  
J = loss_function.forward(y=0, pred=0.3)  
print(f"y=0, pred=0.3 -> J = {J:.4f}")

'''
y=0, pred=0.3 -> J = 0.3567
'''

Visualization

preds = np.arange(start=0.1, stop=1, step=0.01)  
case1 = [loss_function.forward(y=0, pred=i) for i in preds]  
case2 = [loss_function.forward(y=1, pred=i) for i in preds]  
  
fig, axes = plt.subplots(ncols=2, figsize=(12, 6))  
axes[0].plot(preds, case1)  
axes[0].set_title('case.1 y=0'); axes[0].set_xlabel('preds'); axes[0].set_ylabel('loss')  
  
axes[1].plot(preds, case2)  
axes[1].set_title('case.2 y=1'); axes[1].set_xlabel('preds'); axes[1].set_ylabel('loss')  
  
plt.show()

---

Differentiation

#️⃣ 평균 변화율(Average Rate of Change)

함수가 일때,

ex.1) x0=2, x1=3에 대해 구간 [x0, x1]에서의 평균 변화율은?

ex.2) x0=0, x1=3에 대해 구간 [x0, x1]에서의 평균 변화율은?

ex.3) x0=-2, x1=1에 대해 구간 [x0, x1]에서의 평균 변화율은?

ex.4) x0=-3, x1=3에 대해 구간 [x0, x1]에서의 평균 변화율은?

#️⃣ Secant Line

Secant Line은 좌표평면 상의 두 점을 지나는 직선을 의미
x0=0, x1=2로 주어졌을 때, (x0, y0)과 (x1, y1)을 지나는 선을 Secant Line 이라고 함

즉, 평균변화율은 secant line의 기울기

y= x2

1. x0=2, x1=3의 기울기 : 5

#️⃣ 평균 변화율

평균 변화율 = Secant Line의 기울기
가 주어졌을 때의 평균 변화율 수식

(미분학에서는 이 표현이 자주 사용됨)

아래와 같은 함수일때 평균 변화율 구하기

ex.1) = 1일때의 평균 변화율

ex.2) = -1일때의 평균 변화율

ex.3) = -2일때의 평균 변화율

#️⃣ Tangent Line

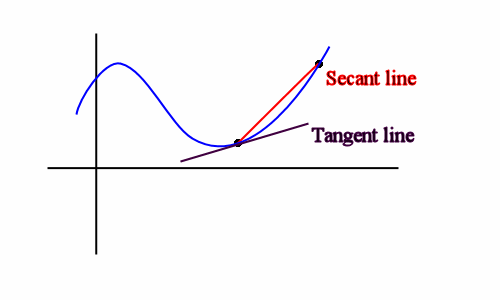
탄젠트 라인은 주어진 점을 지나며 함수에 접하는 직선

가 줄어들 때, secant line(평균 변화율)의 기울기는 점점 tangent line의 기울기와 비슷해짐

특정 에서의 tangent line의 기울기를 로 나타내고
이를 에서의 접선의 기울기(tangent line) = 순간 변화율 = 즉 미분계수라고 부름

#️⃣ 순간 변화율을 활용해 미분계수 구하기

Instantenous rate of change

ex.1) = 2일때의 미분 계수
=4

ex.2) = -1일때의 미분 계수
=-2

ex.3) = 0일때의 미분 계수
=0

#️⃣ 도함수의 정의

미분계수를 구하고자 하는 x를 f’(x)에 입력하면 해당 x에 대한 미분계수를 출력함

#️⃣ 편미분

참고

• 편미분은 다변수 함수에서 한 변수를 대상으로 미분하는 것
• = f를 x에 대해 편미분
• x이외의 변수들은 상수로 취급하여 미분할 때 0이 됨
• bias로 편미분할 경우에 bias 빼고 전부다 0이 됨 (중요)

#️⃣ Backpropagation을 위한 미분

오차역전파에서는 인공뉴런을 통과하면서 생긴 값의 각 미분 값을 가지고 있다가,
loss의 미분값을 backward로 돌아가면서 순차적으로 곱해서 직전노드의 weight과 bias의 미분값에 최종적으로 곱해서 parameters를 업데이트함

오차역전파 학습을 위해 우선 각 value의 미분값을 구하는 계산을 확인하도록 함

• derivatives of “affine function”

• derivatives of “sigmoid function”

이 상태에서 합성함수의 미분을 함

그리고 시그모이드로 치환을 위해 오른쪽 분수의 분자에 +1 -1을 추가함

• derivatives of “Binary Crossentropy”

• backpropagation process

앞서 구한 affine, sigmoid, bceloss의 값은 아래와 같음

backpropagation은 위 그림 과 같이 진행됨

1. 파란색 (3번) Loss function에서 계산된 loss의 미분값을 구함
2. 그 값을 초록색 (2번) sigmoid의 미분값에 곱함
3. 곱한 값을 빨간색 (1번)의 w1, w2, b에 대해 편미분한 값에 각각 곱함
4. 그 값을 기존의 w1, w2, b에서 뺌

이건 내일 정리하자…