2023-11-09 46th Class
Artificial Neuron
#️⃣ Artificial Neuron
인공뉴런 함수 적용 과정
x → Artificial Neuron → y
- x 는 vector라는 의미
인공뉴런 함수 적용 과정 상세
x → Affine Function → Activation Function → y
- 위의 함수 식을 수식으로 표현하면
- y = Activation Function(Affine Function(x)) 와 같음
- artificial neuron은 affine function과 activation function의 합성함수로 모델링 함
#️⃣ Affine Function
- z = w1x2 + w2x2 + b
- z는 affine value
- x1, x2: 입력
- w1, w2: 입력에 각각 곱해지는 값 = weight (가중치)
- b: 식에 더해지는 값
ex. 1) w1 = 1, w2 = 1, b = -1.5 인 경우
x1=0, x2=0 -> z = 1x0 +1x0 -1.5 = -1.5
x1=0, x2=1 -> z = 1x0 + 1x1 -1.5 = -0.5
x1=1, x2=0 -> z = 1x1 + 1x0 -1.5 = -0.5
x1=1, x1=1 -> z = 1x1 + 1x1 -1.5 = 0.5
⬇
(x1, x2) = (1, 1)의 경우에만 양수이고, 나머지의 경우는 음수
즉 위의 affine func는 AND GATE
Affine Function의 수식
는 벡터의 내적 (dot product)로 원소끼리 곱해서(hadamard product) Summation을 함
#️⃣ Activation Function
활성화 함수로,
affine function의 결괏값 z를 입력값으로 받아서 최종 출력값을 결정하는 함수
ex) Sigmoid, ReLU, tanh 등
Sigmoid Function
| graph | formula |
|---|---|
 |
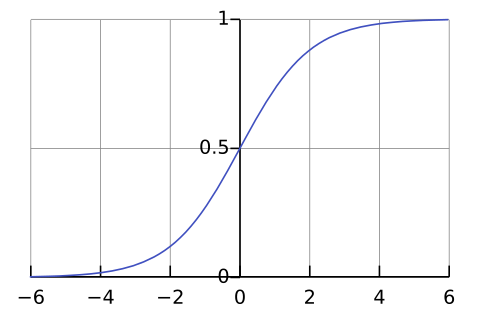$$y = \frac{1}{1+e^{-x}}$$ |
특징
- 실수 전체의 입력을 받아 0~1 사이의 값으로 출력한다 (확률로 해석 가능)
- 실수 전체의 x 중에서 -3보다 작으면 함숫값은 0으로, 3보다 크면 함숫값은 1로 생각할 수 있음
- 유의미한 함숫값의 변화를 만드는 구간은 실수 전체의 x 중에서 상당히 좁음(-3 ~ 3)
- (0, 0.5)를 지남
- x가 0보다 작으면 함숫값은 0.5보다 작아지고, x가 0보다 크면 함숫값은 0.5보다 커짐
- weight, bias가 없음
- y=0, y=1이 점근선
점근선: 그래프가 한없이 가까워지는 직선
ex) x->일때 y -> 1이면 x가 커질수록 y 값은 1에 수렴하는것이고
1에 닿지는 않지만 1에 계속 다가가는 것 -> 이때 y=1 직선을 점근선이라고 하는 것
최종 결과가 0~1 사이 값을 출력하기 때문에 Sigmoid는 binary classification에 사용됨
#️⃣ Code
Affine Function
class AffineFunction:
def __init__(self, w, b):
self.w = w
self.b = b
def forward(self, x):
affine = np.dot(self.w, x) + self.b
return affine
affine1 = AffineFunction(np.array([1, 1]), -1.5)
print(f"{affine1.w=}, {affine1.b=}")
vec1 = np.array([0, 1])
print(f"{affine1.forward(vec1)=}")
affine2 = AffineFunction(np.array([-1, -1]), 0.5)
print(f"{affine2.w=}, {affine2.b=}")
vec2 = np.array([0, 0])
print(f"{affine2.forward(vec2)=}")
'''
affine1.w=array([1, 1]), affine1.b=-1.5
affine1.forward(vec1)=-0.5
affine2.w=array([-1, -1]), affine2.b=0.5
affine2.forward(vec2)=0.5
'''
Sigmoid Function
class Sigmoid:
def forward(self, z):
return 1 / (1 + np.exp(-z))
sigmoid = Sigmoid()
print(f"{sigmoid.forward(-5)=}")
print(f"{sigmoid.forward(-3)=}")
print(f"{sigmoid.forward(0)=}")
print(f"{sigmoid.forward(3)=}")
print(f"{sigmoid.forward(5)=}")
'''
sigmoid.forward(-5)=0.0066928509242848554
sigmoid.forward(-3)=0.04742587317756678
sigmoid.forward(0)=0.5
sigmoid.forward(3)=0.9525741268224334
sigmoid.forward(5)=0.9933071490757153
'''
plot sigmoid function
fig, ax = plt.subplots(figsize=(6, 2.5))
x_data = np.linspace(-5, 5, 100)
y_data = sigmoid.forward(x_data)
# line chart
ax.plot(x_data, y_data)
# vertical & horizontal lines
ax.axvline(x=0, ymin=0, ymax=1, color='gray', linewidth=1)
ax.axhline(y=0, xmin=0, xmax=1, color='gray', linewidth=1)
ax.set_title("Sigmoid Function")
plt.show()
정리
Affine Function: 특정 패턴을 추출하여 추출하고자 하는 패턴이라면 양수, 아니면 음수를 출력
Sigmoid Function: 양수는 0.5보다 큰 값, 음수는 0.5보다 작은 값으로 만듦
입력받은 양수가 3보다 크면 1을 출력
입력받은 음수가 -3보다 작으면 0을 출력
따라서, Artificial Neuron은 특정 패턴을 입력받아 추출하고자 하는 패턴을 입력받으면 1, 아니면 0을 출력하는 함수
artificial neuron
class ArtificialNeuron:
def __init__(self, w, b):
self.affine = AffineFunction(w, b)
self.sigmoid = Sigmoid()
def forward(self, x):
z = self.affine.forward(x)
output = self.sigmoid.forward(z)
return output
an = ArtificialNeuron(np.array([0.5, 0.5]), -0.7)
print(f"{an.forward(np.array([1, 1]))=}")
'''
an.forward(np.array([1, 1]))=0.574442516811659
'''
Multi Layer Perceptron
#️⃣ Multi Layer
- 입력 x는 neuron 1, 2, 3에 모두 입력
- 각 neuron은 weight, bias가 다르기 때문에 서로 다른 패턴을 추출하여 각각 0 또는 1을 출력
- neuron 1-1(초록) 입장에서 n개의 입력이 있다면 n개의 weight 입력 + 1개의 bias 총 n+1 개의 파라미터가 존재
- neuron 2-1(오렌지) 는 2번째 layer
- deep neural network는 여러개의 layer(층)을 가진 신경망
multi neurons
class Model:
def __init__(self):
self.and_gate = ArtificialNeuron(w=np.array([0.5, 0.5]), b=-0.7)
self.or_gate = ArtificialNeuron(w=np.array([0.5, 0.5]), b=-0.2)
self.nand_gate = ArtificialNeuron(w=np.array([-0.5, -0.5]), b=0.7)
def forward(self, x: np.ndarray):
a1 = self.and_gate.forward(x)
a2 = self.or_gate.forward(x)
a3 = self.nand_gate.forward(x)
return np.array([a1, a2, a3])
model = Model()
print(f"{model.forward(np.array([0, 1]))=}")
'''
model.forward(np.array([0, 1]))=array([0.450166 , 0.57444252, 0.549834 ])
'''
#️⃣ weight & bias in MLP
[1] 뉴런 1개의 관점
- 뉴런 = weight vector + scalar bias
- 각 뉴런은 n개의 요소를 가진 '가중치 벡터 w’와 '편향 스칼라 b’를 포함
- b는 bias의 줄임말로, 수학에서는 절편에 해당하지만 딥러닝에서는 편향이라고 부름
- n = 이전 층의 입력값 개수 (혹은 뉴런의 개수)
위 예시에서는 뉴런이 3개이고, 각 뉴런마다 (n, ) 짜리 w와 (1,) 짜리 b가 1세트씩 총 3 세트가 있음
[2] 레이어 층의 관점
<가중치 매트릭스>
- 3개의 뉴런의 가중치 벡터 w를 오른쪽으로 연속해서 붙이게되면 (n, 3) 짜리 행렬 모양이 만들어짐
- 이것을 가중치 매트릭스 W 라고 부름 (weight matrix)
- 가중치 매트릭스 W의 내부의 원소를 보면,
- w11은 1번째 뉴런의 1번째 가중치
- w12는 2번째 뉴런의 1번째 가중치
- w13은 3번째 뉴런의 1번째 가중치
<편향 벡터>
- 3개의 뉴런의 편향 스칼라를 붙이게 되면 (3, ) 짜리 벡터 모양이 만들어짐
- 이것을 편향 벡터 b 라고 부름 (bias vector)
- 편향 벡터 b의 내부의 원소를 보면,
- b1은 1번째 뉴런의 편향
- b2는 2번째 뉴런의 편향
- b3은 3번째 뉴런의 편향
즉 W, b는 해당 층의 모든 weight과 bias를 한 번에 표현한 것
[3] 행렬 계산 관점
행렬을 통해 현재 레이어 층의 모든 연산을 수행하는 방법 (위의 수식)
-
=
전치된 가중치 행렬 x 입력 벡터를 곱 + 편향 -
전치된 가중치 행렬 x 입력 벡터
- 가중치 행렬 (
) 은 원래 세로로 된 벡터가 오른쪽으로 쌓인 형태이었음 - 하지만 (n,3)인 가중치 행렬과, (n,)인 입력 벡터의 내적을 구하려면 모양이 맞아야 함
- ->
에서 T는 전치 행렬로 주 대각선을 축으로 뒤집은 것 (그림 참고) - -> (n,3)인 가중치 행렬을 전치하면 (3,n)으로 바뀌게 되어서 (n,)인 입력벡터와 곱할 수 있게 됨
- 참고: 행렬을 곱하고싶다면(hadamard) 안쪽 값이 같아야 함 ex) (3,n) x (n,1) = (3,n)
- -> hadamard product 이후에는 summation을 하면 내적 벡터 = (3,) 가 됨
- 가중치 행렬 (
-
(전치된 가중치 행렬 x 입력 벡터) + 편향
- (3,1)이 된
에 bias vector (3,)를 더함 - -> 최종 : (3,1) 짜리 output 도출
- (3,1)이 된
#️⃣ parameter의 개수
- 총 파라미터가 많을 수록 모델의 complexity 증가 (모델이 복잡하다는 의미)
ex) n개의 입력, 3개의 뉴런이 있는 경우
1개의 뉴런 당 w: n개, b:1개 -> n+1개
레이어의 파라미터 수는 3 x (n+1) 개
총 파라미터 개수 구하기 예제
2 번째 레이어 weight=m2xm1, bias=m2, 총파라미터=m2(m1+1)
3 번째 레이어 weight=m3xm2, bias=m3, 총파라미터=m3(m2+1)
- 이전 층의 뉴런 개수가 input (n)
- weight 개수는 이전 층 뉴런 수 x 현재 층 뉴런 수
- bias는 현재 층 뉴런수
- 따라서 총 파라미터 수는 (이전 층 뉴런 수 x 현재 층 뉴런 수) + 현재 층 뉴런 수