728x90
❤️ 배운 것
ML 관련 수학
Mean Subtraction: 평균 값을 구하고, 그 평균을 각 값에서 뺀 다음에 평균을 구하면 0이 된다.
# 평균 값을 구하고, 그 평균을 각 값에서 뺀 다음에 평균을 구하면 0이됨
score1 = 10
score2 = 20
score3 = 30
n_student = 3
score_mean = (score1 + score2 + score3) / n_student
score1 -= score_mean
score2 -= score_mean
score3 -= score_mean
score_mean = (score1 + score2 + score3) / n_student분산(variance): 데이터가 얼마나 퍼져있는지(편차 제곱의 평균) 구하는 방법 => 제곱의 평균 - 평균의 제곱 (제평-평제 or MOS - SOM)
표준편차(standard deviation): 분산의 제곱근
scores = [10, 20, 30]
n_student = len(scores)
mean = (scores[0] + scores[1] + scores[2]) / n_student
mean_of_square = (scores[0]**2 + scores[1]**2 + scores[2]**2) / n_student # (각 항목의) 제곱의 평균
square_of_mean = mean**2 # 평균의 제곱
variance = mean_of_square - square_of_mean # MOS - SOM
std = variance**0.5 # square root of the variancestandardization: 평균이 0 분산이 1인 표준 정규분포로 변환하는 것
scores[0] = (scores[0] - mean)/std
scores[1] = (scores[1] - mean)/std
scores[2] = (scores[2] - mean)/stdvector norm: 벡터의 길이
2차원에서 피타고라스 정리를 활용해 norm(c)을 구할 수 있음
$$ \begin{aligned} c^2 = a^2 + b^2\
c = \sqrt{a^2 + b^2} \end{aligned} $$
3차원(v1, v2, v3)에서 피타고라스 정리를 활용해 norm을 구할 수 있음
(가로, 세로, 높이) 라고 하면
1) v1, v2축 평면의 좌표는 (v1, v2)이고 이 점의 길이 a는
$$a = \sqrt{v_1^2+v_2^2}$$
2) v2, v3축 평면의 좌표는 (v2, v3)이고 이 점의 길이 b는 높이 v3임
3) 따라서 $$d = \sqrt{(v_1^2+v_2^2) + v_3^2}$$
vector norm 수식을 일반화 하면 아래와 같음
$$||\overrightarrow{v}|| = \sqrt{\displaystyle\sum_{i=0}^{n}{v_i^2}}$$
v1 = [1, 2, 3]
norm = (v1[0] ** 2 + v1[1] ** 2 + v1[2] ** 2) ** 0.5unit vector: 크기가 1인 벡터 좌표의 스케일링을 1로 했다고 생각하면 됨
v1 = [v1[0]/norm, v1[1]/norm, v1[2]/norm]
norm = (v1[0]**2 + v1[1]**2 + v1[2]**2) ** 0.5dot product (내적): 같은 인덱스의 원소끼리 곱해서 더하는 것. 결괏값은 scalar(숫자) 같은 인덱스의 원소끼리 곱하기만 하는 것은 hadamard $$\overrightarrow{v} \circ \overrightarrow{c}$$ > v 화살표는 v=[1, 2, 3] 같은 리스트(벡터)라는 의미
$$\overrightarrow{v}\cdot\overrightarrow{u} = \displaystyle\sum_{i=0}^{n}{v_i \times u_i }$$
v1, v2 = [1, 2, 3], [3, 4, 5]
dot_prod = 0
dot_prod += v1[0]*v2[0]
dot_prod += v1[1]*v2[1]
dot_prod += v1[2]*v2[2]내적은 cosine similarity와 관계가 있음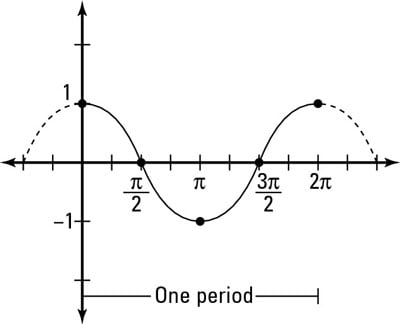
- 코사인 그래프의 치역은 -1~1
- cosine 값은 밑변/빗변
- 코사인 값이 높을수록 각도(theta)가 작고, 두 벡터가 유사하다는 의미
- ex ) 두 벡터가 포개질때는 사잇각이 0°이고 위의 그래프에서는 값이 1이 나옴 -> 가장 유사(똑같을때)하면 y값이 1이 나옴
euclidean distance: 두 점 사이에 선을 그었을 때의 길이. L2 distance라고 함 (L1 거리는 Manhattan distance) euclidean distance는 가장 가까운 N개의 값을 골라내는 KNN에 쓰임

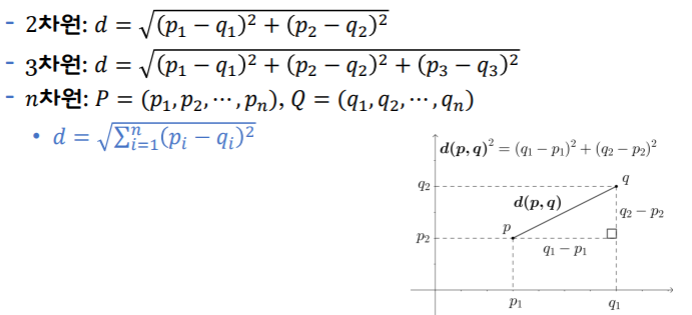
mean squared error: 예측값에서 정답값을 뺀 값의 제곱을 누적해 더한 값의 평균으로 구하는 오차
$$J = \frac{1}{n} \displaystyle\sum_i^n{ℒ^{(i)}} = \frac{1}{n} \displaystyle\sum_i^n{(\hat{y}^{(i)} - y^{(i)})}^2$$
pred1, pred2, pred3 = 10, 20, 30
y1, y2, y3 = 10, 25, 40
n_data = 3
s_error1 = (pred1 - y1)**2
s_error2 = (pred2 - y2)**2
s_error3 = (pred3 - y3)**2
mse = (s_error1 + s_error2 + s_error3) / n_data💛 배운점/느낀점
- ML 관련 수학 개념의 원리와 수식 -> 코드로 구현하는 실습을 하여 유익했다.
- 코사인유사도나 KNN에서 도출되는 값의 기전을 알 수 있는 기회가 되어서 좋았다.
- Latex를 markdown에 사용하는 방법을 익혔다.. ㅎ.ㅎ!!
반응형
'Education > 새싹 TIL' 카테고리의 다른 글
| 새싹 AI데이터엔지니어 핀테커스 4주차 (목) - ML 관련 수학 (3) (0) | 2023.09.21 |
|---|---|
| 새싹 AI데이터엔지니어 핀테커스 4주차 (수) - ML 관련 수학 (2) (0) | 2023.09.20 |
| 새싹 AI데이터엔지니어 핀테커스 4주차 (월) - Math in Python (0) | 2023.09.18 |
| 새싹 AI데이터엔지니어 핀테커스 3주차 (목) - visualization (0) | 2023.09.14 |
| 새싹 AI데이터엔지니어 핀테커스 3주차 (수) - pandas(3), matplotlib (0) | 2023.09.14 |